FERRY: RANGKUMAN BAB 9 - 12 SISTEM CERDAS

(9)

INFERENSI DALAM LOGIKA ORDER PERTAMA

· Mengubah inferensi order pertama menjadi inferensi proposisi

KETERBATASAN LOGIKA PROPOSISI

- Perhatikan contoh berikut :

All men are mortal

Socrates is a man

__________________________

Therefore, Socrates is mortal

Misal : p = All men are mortal

q = Socrates is a man

r = Socrates is mortal

Skema argumennya menjadi : p, q; r

_______

Bila dibuat tabel kebenaran, hasilnya invalid.

- Argumen invalid sering diinterpretasikan sebagai konklusi yang salah (walaupun beberapa orang berpendapat argumen itu dapat saja bernilai benar).

- Argumen yang invalid berarti argumen tersebut tidak dapat dibuktikan dengan logika proposisi.

- Keterbatasan logika proposisi dapat diatasi melalui logika predikat sehingga argumen tersebut menjadi valid.

- Kenyataannya, semua logika silogistik adalah subset yang valid dari logika proposisi urutan pertama.

Contoh :

If Socrates is a man, then Socrates is mortal

Socrates is a man

Therefore, Socrates is mortal

Misal:

p = Socrates is a man

q = Socrates is mortal

Argumennya menjadi :

p →q

_______________

Argumen di atas adalah silogistik yang valid, yaitu bentuk

modus ponens.

· Generalized Modus ponens

Banyak teknik AI didasarkan pada logika predikat, diperpanjang dengan cara tertentu, menggunakan modus umum ponens sebagai aturan inferensi. Hal ini sederhana untuk program dan cukup kuat. Bahasa pemrograman Prolog didasarkan pada semacam logika ini.

· FORWARD CHAINING DAN BACKWARD CHAINING

Metode forward Chaining

Kadang disebut:data-driven karena inference engine menggunakan informasi yang ditentukan oleh user untuk memindahkan ke seluruh jaringan dari logika ‘AND’ dan ‘OR’ sampai sebuah terminal ditentukan sebagai objek. Bila inference engine tidak dapat menentukan objek maka akan meminta informasi lain. Aturan (Rule) di mana menentukan objek, membentuk path (lintasan) yang mengarah ke objek. Oleh karena itu, hanya satu cara untuk mencapai satu objek adalah memenuhi semua aturan.

Forward chaining: Pencocokan fakta atau pernyataan dimulai dari bagian sebelah kiri dulu (IF dulu). Dengan kata lain penalaran dimulai dari fakta terlebih dahulu untuk menguji kebenaran hipotesis.

Metode backward Chaining

Merupakan kebalikan dari forward chaining dimana mulai dengan sebuah hipotesa (sebuah objek) dan meminta informasi untuk meyakinkan atau mengabaikan. Backward chaining inference engine sering disebut: ‘Object-Driven/Goal-Driven‘.

Catatan: inference engine adalah bagian dari sistem pakar yang mencoba menggunakan informasi yang diberikan untuk menemukan objek yang sesuai. Inference engine mempunayi 2 kategori yaitu deterministic dan probabilistik. Sedangkan dasar untuk membentuk inference engine diantaranya: forward chaining, backward chaining dan rule value (merupakan pendahulu dari forward dan backward chaining).

Backward Chaining: Pencocokan fakta atau pernyataan dimulai dari bagian sebelah kanan (THEN dulu). Dengan

kata lain penalaran dimulai dari hipotesis terlebih dahulu, dan untuk menguji kebenaran

hipotesis tersebut harus dicari fakta-fakta yang ada dalam basis pengetahuan.

Contoh forward dan backward chaining dikutip dari Idhawati Hestiningsih

R1 : IF suku bunga turun THEN harga obligasi naik

R2 : IF suku bunga naik THEN harga obligasi turun

R3 : IF suku bunga tidak berubah THEN harga obligasi tidak berubah

R4 : IF dolar naik THEN suku bunga turun

R5 : IF dolar turun THEN suku bunga naik

R6 : IF harga obligasi turun THEN beli obligasi

(10)

PENALARAN

· KETIDAKPASTIAN

PENALARAN DENGAN KETIDAKPASTIAN (UNCERTAINITY) KETIDAKPASTIAN (Uncertainity)

- Ketidakpastian dapat dianggap sebagai suatu kekurangan informasi yang memadai untuk membuat suatu keputusan.

- Ketidakpastian merupakan suatu permasalahan karena mungkin menghalangi kita membuat suatu keputusan yang terbaik.

- Teori-teori yang berhubungan dengan ketidakpastian :

= Probabilitas Klasik

= Probabilitas Bayes

= Teori Hartley yang berdasarkan pada himpunan klasik

= Teori Shanon yang didasarkan pada peluang

=Teori Dempster-Shafer

= Teori Fuzzy Zadeh

- Contoh aplikasi yang klasik sistem pakar yang sukses sehubungan dengan ketidakpastian :

= MYCIN untuk diagnosa medis

= PROPECTOR untuk ekplorasi mineral

· PROBABILITAS

TEORI PROBABILITAS

- Teori formal probabilitas dibuat dengan menggunakan 3 aksioma

- Teori aksiomatik disebut juga objective theory of probability diperkenalkan oleh Kolmogorov, sedangkan teori aksiomatik probabiliti kondisional dibuat oleh Renyi.

PROBABILITY KLASIK

- Probability merupakan cara kuantitas yang berhubungan dengan ketidakpastian

- Teori probability diperkenalkan pada abad 17 oleh penjudi Perancis dan pertama kali diajukan oleh Pascal dan Fermat (1654)

- Prob. Klasik disebut juga dengan a priori probability karena berhubungan dg game atau sistem.

- Formula fundamental prob. Klasik

P = W / N

dimana :

W = jumlah kemenangan

N = jumlah kemungkinan kejadian yang sama pada percobaan

TEOREMA BAYES

- Ditemukan oleh Thomas Bayes

- Teorema Bayes kebalikan dari probabilitas kondisional P(A|B) atau disebut posteriori probability, dimana dalam teorema Bayes : state probabilitas dari kejadian awal diberikan untuk melihat kejadian yang mungkin akan terjadi

kemudian.

Dari contoh kerusakan disket merk X dan bukan merk X :

- (6) 75% kemungkinan disket merk X akan rusak dlm 1

tahun adalah.

- (7) probabilitas disket merk bukan X rusak dalam 1

tahun 50%.

- Pertanyaannya adalah : kita punya disket dan tidak tahu merk apa, bagaimana probabilitas kerusakannya jika merk X ? Atau merk bukan X ?

- Bentuk umum Teorema Bayes : P(Hi|E) = P(EÇHi)

å j P(EÇHj)

= P(E|Hi) P(Hi)

å j P(E|Hj) P(Hj)

= P(E|Hi) P(Hi)

P(E)

· FAKTOR KEPASTIAN

Faktor Kepastian (Certainty Factor)

Faktor kepastian merupakan cara dari penggabungan kepercayaan (belief) dan ketidapercayaan (unbelief) dalam bilangan yang tunggal. Dalam certainty theory, data-data kualitatif direpresentasikan sebagai derajat keyakinan (degree of belief).

Tahapan Representasi Data Kualitatif

Tahapan dalam merepresentasikan data-data kualitatif :

- kemampuan untuk mengekspresikan derajat keyakinan sesuai dengan metode yang sudah dibahas sebelumnya.

- kemampuan untuk menempatkan dan mengkombinasikan derajat keyakinan tersebut dalam sistem pakar.

Dalam mengekspresikan derajat keyakinan digunakan suatu nilai yang disebut certainy factor (CF) untuk mengasumsikan derajat keyakinan seorang pakar terhadap suatu data.

Dimana :

- CF = Certainy Factor (faktor kepastian) dalam hipotesis H yang dipengaruhi oleh fakta E.

- MB=Measure of Belief (tingkat keyakinan), adalah ukuran kenaikan dari kepercayaan hipotesis H dipengaruhi oleh fakta E.

- MD=Measure of Disbelief (tingkat ketidakyakinan), adalah kenaikan dari ketidakpercayaan hipotesis H dipengaruhi fakta E.

- E = Evidence (peristiwa atau fakta).

- H = Hipotesis (Dugaan).

· TEORI DEMPSTER – SHAFER

Teori Dempster-Shafer adalah teori matematika untuk pembuktian berdasarkan belief functions(fungsi kepercayaan) dan plausible reasonin (penalaran yang masuk akal). Digunakan untuk mengkombinasikan potongan informasi (fakta) yang terpisah untuk mengkalkulasi kemungkinan dari suatu peristiwa.Teori Dempster-Shafer adalah suatu teori matematika untuk pembuktian (Kusumadewi, 2003) berdasarkan belief functions and plausible reasoning (fungsi kepercayaan dan pemikiran yang masuk akal), yang digunakan untuk mengkombinasikan potongan informasi yang terpisah (bukti) untuk mengkalkulasi kemungkinan dari suatu peristiwa. Teori ini dikembangkan oleh Arthur P. Dempster dan Glenn Shafer.

Ada berbagai macam penalaran dengan model yang lengkap dan sangat konsisten, tetapi pada kenyataannya banyak permasalahan yang tidak dapat terselesaikan secara lengkap dan konsisten. Ketidakkonsistenan yang tersebut adalah akibat adanya penambahan fakta baru. Penalaran yang seperti itu disebut dengan penalaran non monotonis. Untuk mengatasi ketidakkonsistenan tersebut maka dapat menggunakan penalaran dengan teori Dempster-Shafer. Secara umum teori Dempster-Shafer ditulis dalam suatu interval:

Belief,Plausibility

Belief (Bel) adalah ukuran kekuatan evidence dalam mendukung suatu himpunan proposisi. Jika bernilai 0 maka mengindikasikan bahwa tidak ada evidence, dan jika bernilai 1 menunjukkan adanya kepastian. Dimana nilai bel yaitu (0-0.9).

Plausibility (Pl) dinotasikan sebagai : Pl(s) = 1 – Bel (-s) Plausibility juga bernilai 0 sampai 1. Jika yakin akan-s, maka dapat dikatakan bahwa Bel(-s)=1, dan Pl(-s)=0.

Contoh :

Diketahui nilai belief adalah 0,5 dan nilai plausibility adalah 0,8 untuk proposisi “the cat in the box is dead”

Bel = 0,5

Fakta yang mendukung proposisi tersebut memiliki nilai kepercayaan sebesar 0,5

Pl = 0,8

Fakta yang melawan proposisi tersebut hanya memiliki nilai kepercayaan sebesar 0,2

(11)

BAHASA PEMROGRAMAN UNTUK APLIKASI INTELEGENSI BUATAN

· DASAR-DASAR PROLOG

Fakta dan Relasi

Fakta Adalah suatu unit yang selalu bernilai benar,fakta ini merupakan kumpulan data-data objek. Suatu fakta dibedakan dalam 2 jenis, yaitu fakta yang menunjukan relasi dan fakta yang menunjukan milik/sifat, penulisan suatu fakta selalu di akhir dengan (.)

Contoh :

Fakta	Prolog
Slamet adalah ayah Amin	ayah (slamet, amin).
Anita adalah seorang wanita	wanita (anita).
Angga suka renang dan tenis	suka(angga,renang).dan suka(angga,tenis).
Jeruk berwarna jingga	jngga(jeruk).

Aturan (“Rules”)

Aturan adalah suatu pernyataan yang menunjukan bagaimana fakta-fakta berinteraksi satu dengan yang lain untuk membentuk suatu kesimpulan. Sebuah aturan dinyatakan sebagai suatu kalimat bersyarat. Kata “if” adalah kata yang dikenal Prolog untuk menyatakan kalimat bersyarat atau disimbolkan dengan “:-“.

Contoh :

Fakta dan Aturan	Prolog
F : Tino suka apel A : Yuli suka sesuatu yang disukai Tino	suka(tino, apel). suka(yuli,Sesuatu) :- suka(tino,Sesuatu).

Pertanyaan (“Query”)

Setelah memberikan data-data berupa fakta dan aturan, selanjutnya kita dapat mengajukan pertanyaan berdasarkan fakta dan aturan yang ada. Penulisannya diawali simbol “?-“ dan diakhiri tanda “.”.

Contoh :

Pertanyaan	Prolog dan Jawaban Program
Apakah Tini suka boneka ?	?- suka(tini,boneka). Yes ……. (jika faktanya Tini suka boneka) No……..…(jika tidak sesuai fakta).
Apakah yang disukai Tini ?	?- suka(tini,Apa). Apa=boneka
Siapakah yang suka boneka ?	?- suka(Siapa,boneka). Siapa=tini
Dari contoh silsilah keluarga di atas : Siapakah kakek Budi ? Siapakah cucu Slamet ?	?- kakek(Siapa,budi). Siapa=slamet ?- kakek(slamet,Cucu). Cucu=budi ; Cucu=badu (jika kemungkinan ada lebih dari satu jawaban gunakan tanda “;” pada akhir setiap jawaban).

· STRUKTUR PROGRAM PROLOG

Dalam struktur program prolog terdapat 4 macam di antara nya adalah Domain,Predicate,Variable, dan goal.

Domain

Domain berfungsi untuk menyatakan jenis suatu variabel seperti hal nya tipe data dalam bahasa prosedural (Pascal,C) . beberapa domain standar dalam prolog diantara nya char,integer,real,string,symbol. Contoh :

namaBunga = symbol

mataKuliah = string

nilai = integer

- Domains char dipakai pada predikat yang argumennya memiliki nilai berupa karakter tunggal, yaitu abjad, angka, pungtuasi (?.!,<,...), dan operasi (+,‐,...). Penulisan argumen bertipe char dalam prolog diapit tanda ’...’. contoh : nilai (dita, ’A’).

- Domains string dipakai pada predikat yang argumennya memiliki nilai berupa karakter jamak yang dapat berupa kata maupun suatu tulisan (kumpulan kata‐kata termasuk di dalamnya pungtuasi dan tanda operasi yang dapat dipisahkan spasi). Penulisan argumen bertipe string dalam prolog diapit tanda ”...”. contoh: hobi(rina,”Memasak”).

-Domains integer dipakai pada predikat yang argumennya memiliki nilai berupa bilangan bulat.

Contoh : nilai(tini,”Kalkulus”,75).

-Domains real dipakai pada predikat yang argumennya memiliki nilai berupa bilangan pecahan. Penulisan argumen bertipe real dalam prolog untuk nilai pecahan ditulis di belakang tanda titik (.). contoh: nilai(ivan, 8.75).

-Domains symbol dipakai pada predikat yang argumennya memiliki nilai berupa kumpulan karakter yang hanya terdiri dari huruf atau kata tanpa dipisahkan oleh spasi. Suatu kata dapat disambungkan dengan kata lain dengan tanda _ (underscore). contoh : lelaki(toni_setiawan).

Predicate

Dalam bahasa prolog kita perlu mendeklarasikan predikat yang ada pada bagian Predicates dan mendefinisikannya dalam bagian Clauses. Jika tidak, Prolog tidak akan mengenalnya. Namun untuk predikat standar seperti cursor, makewindow, readln, readchar dsb tidak perlu dideklarasikan.

Misalkan untuk domains seperti di atas dapat dibuat predicates

Predicates

menu(integer)

data(NamaOrang, Alamat, Umur)

Deklarasi predicates dalam bagian predicates, harus disertai argumen jika memang berargumen. Nama predikat harus diawali dengan huruf, boleh besar atau kecil, selebihnya bisa huruf, angka, garis bawah, namun dianjurkan untuk dimulai dengan huruf kecil. Nama predikat tidak boleh mengandung spasi, tanda minus, asteris atau garis miring.

Variable

Variabel merupakan sebuah interpretasi yang digunakan untuk menemukan

nilai dari sebuah klausa. Variabel harus diawali dengan huruf besar. Contoh :

- suka(andi,X) .

X = eskrim

- anakperempuan(lila, X).

X = agus

Variabel yang memiliki beberapa value kamu dapat memunculkan nilai lain dengan

menekan tombol (;)

Deskripsi Rekrusif dari Sebuah Hubungan

Nah ini yang gak kalah penting, Rekursif ini digunakan untuk mencari seluruh dari

child dari sebuah tree. Intinya, misalkan terdapat sebuah keluarga terdapat kakek,

ayah, dan anak. Maka untuk mendapatkan seluruh keturunan dari kakek, yaitu kakek,

ayah, anak, anaknya anak dan seterusnya kita membutuhkan rekursif.

Representasinya seperti berkut

turunan(X,Y) :- antiturunan(Y,X).

turunan(X,Y) :- antiturunan(Y,Z), turunan(X,Z).

Goal

Goal dalam turbo Prolog ada 2 macam yakni :

a. Goal eksternal

b. Goal internal

Goal eksternal diketikkan langsung pada bagian ‘goal’ : di jendela dialog pada kompiler terpadu Turbo Prolog. dengan cara ini kita hanya bisa menjalankan program dari lingkungan kompiler Turbo Prolog. Untuk dapat dijalankan di lingkungan DOS kita harus menggunakan goal internal yang di simpan pada bagian Goal. Sebenarnya goal inilah yang dicari dan dipanggil pada saat program dijalankan. Jika goal tercapai, program berhenti dengan berhasil, tapi jika sebaliknya, program berhenti dalam keadaan gagal.

Contoh :

Predicates

tulis(string)

Goal

tulis(X),

write(X).

Clauses

tulis(“Bandung”).

tulis(“Yogya”).

tulis(“Jakarta”).

Program ini pertama akan memanggil goalnya, yang terdiri dari sub goal tulis dan write. Ini artinya, goal akan memanggil klausa tulis. Di bagian clauses, terdapat tulis yang berupa fakta. Prolog akan mencarinya dari paling atas, diperoleh tulis(“Bandung”). Ini berarti sub-goal tulis(X) berhasil dengan X terikat dengan nilai “Bandung”. Selanjutnya Prolog membuktikan sub-goal kedua yakni write(X). Ini pasti berhasil dan program berhenti. Jika goal diajukan dari luar (dari jendela Goal, goal internalnya dibuang), kemudian kita tuliskan : tulis(X) [enter], akan tertulis pada layar :

X = Bandung

X = Yogya

X = Jakarta

(12)

STUDI KASUS PROLOG

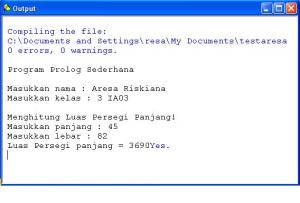
· CONTOH PROGRAM SEDERHANA PROLOG

write(“Program Sederhana Prolog”),nl,nl,

write(“Masukkan nama : “), read(Nama),

write(Nama),nl,

write(“Masukkan kelas : “), read(_kelas),

write(_kelas),nl,nl,

write(“Menghitung Luas Persegi Panjang!”),nl,